Quantumcomputers
Op 30 juni 2021 kwam de planetoïde '2020 AD1' met een relatieve snelheid van ongeveer 17.000 km/h op de aarde af.1 Gelukkig heeft hij de aarde niet geraakt; op 4 juli (de dag van mijn verdediging) schoot de planetoïde voorbij op een afstand van drie keer de afstand tussen de aarde en de maan.
Het zonnestelsel bestaat uit de zon en de objecten in een baan daaromheen. De ons bekende objecten omvatten de planeten, ongeveer een miljoen planetoïden en tientallen ruimteschepen. Met behulp van computers is het mogelijk het zonnestelsel te simuleren. Daartoe wordt er eerst een digitale 'bordspelversie' van het zonnestelsel gemaakt dat enkel de essentiële eigenschappen van het zonnestelsel bevat. In het geval dat we willen voorspellen of een planetoïde de aarde gaat raken, zijn deze eigenschappen de massa, richting, snelheid en positie van de ons bekende objecten in het zonnestelsel. Deze verzameling informatie noemen we vanaf nu de toestand van het zonnestelsel. (De toestand verandert met de tijd.) De spelers op het bordspel stellen de ons bekende objecten in het zonnestelsel voor. Het spel is zo ontworpen dat elke toestand van het spel correspondeert met een toestand van het zonnestelsel. Door vele spelronden te spelen kan een computer de toekomstige speltoestanden uitrekenen en daarmee de toekomstige toestanden van het zonnestelsel. Op deze manier heeft een computer onder andere de toekomstige posities van zowel de aarde als de planetoïde '2020 AD1' uitgerekend. Uit deze berekening blijkt dat deze twee hemellichamen elkaar niet zullen raken in de nabije toekomst.

Afbeelding: De werelden van de klassieke- en quantummechanica. Hoe de klassieke wereld ontstaat uit de quantummechanische is een van de grootste open vragen van de natuurkunde. Voor zover bekend is er geen scherpe grens tussen de twee.
De spelers op het bordspel volgen de spelregels. Deze zijn volkomen deterministisch; voor elke speler is er per beurt één geldige zet. Dit is omdat de spelregels zijn bepaald door de wetten van de klassieke mechanica, en die wetten bieden geen keuzevrijheid. De wetten van de klassieke mechanica zijn ook de natuurwetten die onze alledaagse ervaringen bepalen; als je tegen een pion duwt komt er beweging in, en als je een appel loslaat dan valt hij.
Om de wereld van dit proefschrift te betreden laten we het zonnestelsel achter en zoomen we in op een minuscuul stukje aarde. Ver voorbij de planeten, bomen, mensen, appels, pionnen en micro-organismen betreden we het rijk van de moleculen. Moleculen bestaan uit protonen, neutronen en elektronen. Verrassend genoeg gelden er op deze schaal andere natuurwetten: die van de quantummechanica. Mensen zijn niet gewend aan deze wetten omdat de objecten in ons dagelijks leven de wetten van de klassieke mechanica volgen. Quantummechanica kan daarom tegenintuïtief zijn en staat bekend als ondoorgrondelijk.
Het gedrag van protonen, neutronen en elektronen bepaalt het verloop van chemische reacties. Zou het daarom niet mooi zijn als we ook het gedrag van deze deeltjes kunnen simuleren? We zouden dan beter in staat zijn ingewikkelde chemische reacties te begrijpen, wat weer kan leiden tot de verbetering van bepaalde industriële productieprocessen. De productie van kunstmest is daar een voorbeeld van. De productie van een van de ingrediënten van kunstmest is verantwoordelijk voor ongeveer 1% van het wereldwijde energieverbruik, en dat allemaal in de vorm van fossiele brandstoffen. Er bestaan echter bacteriën die datzelfde ingrediënt produceren zonder het gebruik van fossiele brandstoffen. De simulatie van het chemische proces dat deze bacteriën gebruiken zou ons mogelijk in staat stellen van de bacteriën te leren en daarmee kunstmest milieuvriendelijker te produceren.
De simulatie van elektronen, protonen en neutronen vraagt om een ander bordspel (het 'quantumspel') dan de simulatie van het zonnestelsel. De spelstukken zijn nu de protonen, neutronen en elektronen. Ook de regels van het nieuwe spel zijn anders. Deze worden nu bepaald door de wetten van de quantummechanica. Quantummechanica is niet alleen ingewikkeld voor mensen, maar ook voor computers. Een korte berekening laat zien dat er meer dan 1 Terabyte aan geheugen nodig is om de bordspelversie van 37 elektronen op te slaan. Belangrijker nog is dat dit geheugengebruik verdubbelt met elk elektron dat wordt toegevoegd. Het geheugengebruik groeit daarmee exponentieel in het aantal elektronen. Hierdoor is het onmogelijk om van meer dan een klein aantal elektronen de bordspelversie op te slaan. Om bijvoorbeeld de bordspelversie van meer dan 100 elektronen op te slaan is zelfs de huidige wereldwijde data-opslagcapaciteit niet toereikend. Het lijkt dus praktisch onmogelijk om meer dan 100 elektronen te simuleren.
Maar wat nu als we een computer maken die zelf bestaat uit quantummechanische deeltjes, zoals elektronen, protonen en neutronen? Dat is precies het idee achter de quantumcomputer. Omdat de onderdelen van een quantumcomputer zelf quantummechanische deeltjes zijn, is het voor zo'n computer heel natuurlijk om de bordspelversie van quantummechanische deeltjes op te slaan. Omdat de onderdelen van een quantumcomputer zelf de wetten van de quantummechanica volgen, is het bovendien voor een quantumcomputer heel natuurlijk om de spelregels van het quantumspel toe te passen. Quantumcomputers kunnen daardoor efficiënt quantummechanische systemen simuleren.


Afbeelding: (Boven) Een echte quantumcomputer. In deze afbeelding kijken we door het raam (of eerder een soort patrijspoort) van een vacuümkamer. In het midden van het witte apparaat zweven 14 calcium-ionen. Elk calcium-ion is een natuurlijk voorkomend quantumsysteem, bestaande uit 20 protonen, 20 neutronen en 19 elektronen. Berekeningen worden uitgevoerd door met lasers op de ionen te schijnen. Het 'computerprogramma' dat wordt uitgevoerd bepaalt waar en wanneer de lasers schijnen. Afbeelding: C. Lackner, Universiteit van Innsbruck. (Onder) Close-up van de rij calcium-ionen zoals die in de quantumcomputer gebruikt worden. In werkelijkheid is de breedte van de rij minder dan een halve millimeter. Toch zweven de ionen ver uit elkaar in vergelijking tot hun eigen afmeting; waren de atomen zo groot als een mens geweest, dan zouden ze ongeveer 100 km uit elkaar staan. Afbeelding: Universiteit van Innsbruck.
Quantumcomputers kunnen zelfs meer dan dat; de extra 'quantumkracht' van quantumcomputers kan ook worden aangewend voor het oplossen van puur wiskundige problemen. Een priemgetal is een getal groter dan 1 dat slechts door zichzelf en 1 gedeeld kan worden (zonder rest). De priemgetallen zijn dus 3,5,7,11,... . Het ontbinden in priemfactoren is de taak een gegeven geheel getal te schrijven als product van priemfactoren. Elk getal kan zo ontbonden worden, en deze ontbinding is uniek. Een voorbeeld is 15→3*5. Voor zover bekend is het voor een gewone, klassieke computer onmogelijk efficiënt getallen te ontbinden. Kleine getallen zoals 15 lukken nog, maar klassieke computers bereiken al snel hun limiet. (Dit is omdat de rekentijd exponentieel groeit in het aantal cijfers van het te ontbinden gehele getal.) Daardoor is het onmogelijk getallen te ontbinden met honderden cijfers. Het blijkt echter, dat quantumcomputers in theorie wel efficiënt getallen kunnen ontbinden. (Voor een quantumcomputer groeit de rekentijd niet exponentieel maar als een polynoom in de lengte van het te ontbinden getal.) Ze zouden dus in principe wel in staat kunnen zijn getallen met honderden cijfers te ontbinden.
De veiligheid van de methode die wordt gebruikt voor het versleutelen van berichten die over het internet worden verstuurd, zoals bijvoorbeeld berichten tussen jou en de website van je bank, is gebaseerd op de aanname dat het onmogelijk is getallen met honderden cijfers te ontbinden. Met een quantumcomputer zou je die beveiliging dus kunnen breken. Als slechts enkele landen grote getallen kunnen ontbinden, zou dit onder andere vanwege de spionagepotentie grote gevolgen kunnen hebben voor de wereldwijde machtsbalans. Het onderzoek naar versleutelingsmethoden die zelfs door quantumcomputers niet te breken zijn is daarom ook in volle gang.
Ondanks hun potentie staat de ontwikkeling van quantumcomputers nog in de kinderschoenen. De huidige stand van zaken is dat quantumsuperioriteit of een quantumvoordeel (Engels: 'quantum supremacy' of 'a quantum advantage') is aangetoond op echte quantumcomputers. Dit betekent dat deze quantumcomputers een rekentaak hebben verricht die, voor zover we weten, praktisch onmogelijk is voor klassieke computers. Dit klinkt alsof quantumcomputers nu al volledig de klassieke computers verslagen hebben, maar dat is niet helemaal zo; de rekentaken waarvoor er een quantumvoordeel is aangetoond op echte quantumcomputers zijn artificieel en hebben geen toepassingen (anders dan het aantonen van een quantumvoordeel). Er is tot op heden geen echte quantumcomputer geweest die een nuttige rekentaak heeft uitgevoerd die niet net zo goed op een klassieke computer uitgevoerd had kunnen worden. De mijlpaal van een nuttig quantumvoordeel is dus nog niet bereikt.
Quantumcomputers hebben nog geen nuttig quantumvoordeel bereikt omdat het heel moeilijk is om goede quantumcomputers te bouwen. Het blijkt dat quantumcomputers veel moeilijker dan klassieke computers te beschermen zijn tegen ongewilde invloeden uit hun omgeving. Deze invloeden of 'stoorzenders' bestaan bijvoorbeeld uit magnetische velden of temperatuurschommelingen. In termen van het quantumspel (gebruikt voor het simuleren van quantummechanische systemen op een quantumcomputer) kun je de effecten van deze stoorzenders voorstellen als een onverlaat die op onregelmatige tijden stiekem de quantumcomputer binnendringt en een ongeldige zet doet. Na vele spelronden zal de speltoestand van het bordspel niet langer getrouw de toestand van het gesimuleerde quantummechanische systeem representeren. Het effect van de stoorzenders noemen we ruis, ook al heeft de ruis, net als bijvoorbeeld witte beeldruis op een ouderwetse beeldbuis, misschien niets met geluid te maken. Om in de nabije toekomst een nuttig quantumvoordeel te bereiken is het essentieel dat we de oorzaken en gevolgen van deze ruis goed begrijpen, dat we begrijpen hoe de ruis verminderd kan worden, en dat we begrijpen hoe er met de overgebleven ruis omgegaan kan worden.
Mijn proefschrift
In Hoofdstuk 2 van mijn proefschrift stellen we een rekentaak voor die tegelijk nuttig, moeilijk voor klassieke computers, en geschikt voor de quantumcomputers van de nabije toekomst is. Het uitvoeren van deze taak heeft dus de potentie om een nuttig quantumvoordeel aan te tonen. De taak die we voorstellen is de simulatie van het kagome-rooster. Het is een speciaal type simulatie waar het niet gaat om het voorspellen van toekomstige toestanden maar om het voorspellen van de toestand bij temperaturen rond het absolute nulpunt (-273,15 °C = 0 K).
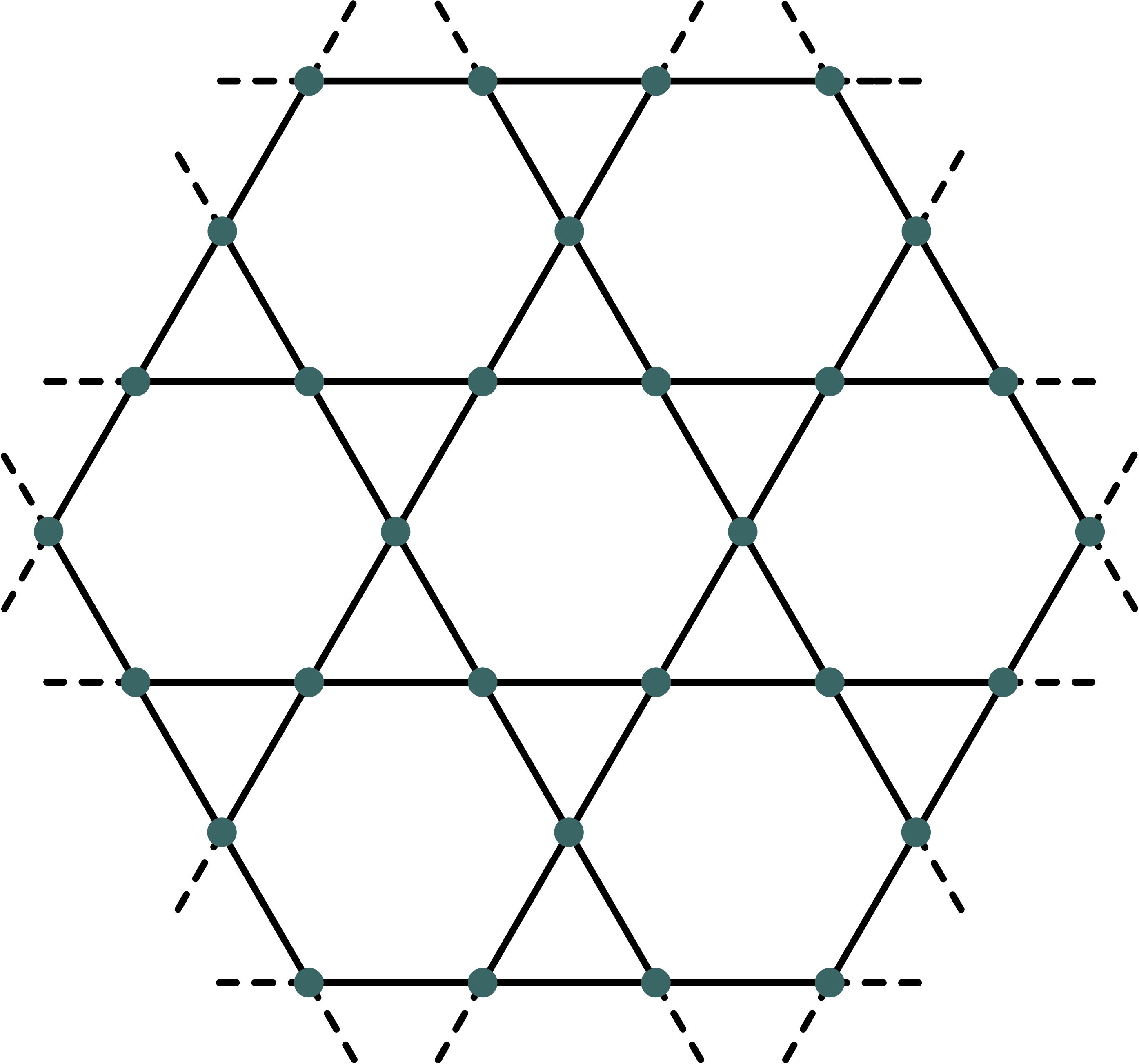

Afbeelding: (Boven) Het kagome-rooster. Op elk kruispunt bevindt zich één elektron. Er treedt een magnetische wisselwerking op tussen elk elektron en zijn buren (met elkaar verbonden door een lijn). De toestand van dit systeem bij temperaturen rond het absolute nulpunt is onbekend. (Onder) Herbertsmithiet, waarvan de magnetische eigenschappen worden beschreven door elektronen op een kagome-rooster. Afbeelding: Bruce Kelley.
De simulatie van het kagome-rooster kan ons nieuwe inzichten geven over de natuur. Er zijn materialen, zoals het mineraal Herbertsmithiet (Engels: Herbertsmithite), ontdekt door - u raadt het al - Herbert Smith, waarvan de magnetische eigenschappen worden beschreven door elektronen op het kagome-rooster. Bij temperaturen rond het absolute nulpunt worden deze eigenschappen nog niet goed begrepen, ondanks decennia aan onderzoek met klassieke computers.
In dit proefschrift ontwerpen we een specifieke simulatiemethode speciaal bedoeld voor de kleine, aan ruis onderhevige quantumcomputers van de nabije toekomst. Deze simulatiemethode noemen we hier het kagome-spel. Het spel is zo gekozen dat het zetten van een enkele zet een quantumcomputer slechts een enkele rekenstap kost. Deze eigenschap is belangrijk voor de quantumcomputers van de nabije toekomst omdat hun berekeningen zo kort mogelijk moeten duren; hoe langer een berekening duurt, hoe meer tijd de stoorzenders hebben om de berekening in de war te gooien. Bovendien is de algemene simulatiemethode die we gebruiken relatief goed bestand tegen ruis.
Om een idee te krijgen van hoe goed onze specifieke simulatiemethode werkt, voeren we deze uit op een kleine quantumcomputer. De quantumcomputer waar we de methode op uitvoeren is echter niet echt; deze wordt zelf gesimuleerd door een klassieke computer. Er is dus sprake van een dubbele simulatie: een klassieke computer simuleert een quantumcomputer die het kagome-rooster simuleert. Deze extra laag simulatie is nodig omdat de quantumcomputer die we nodig hebben om het kagome-spel te testen nog niet bestaat.
Als het onmogelijk is om met klassieke computers het kagome-rooster te simuleren, hoe kan een klassieke computer dan een quantumcomputer simuleren die het kagome-rooster simuleert? Simuleert de klassieke computer dan niet uiteindelijk het kagome-rooster? De kanttekening die hier geplaatst moet worden is dat de quantumcomputer slechts een kleine uitsnede van het kagome-rooster simuleert, met daarop 20 elektronen. De simulatie van die quantumcomputer lukt nog net op een klassieke computer. De simulatie van deze uitsnede op een quantumcomputer is dus niet genoeg voor het aantonen van een quantumvoordeel. Als we echter een wat grotere uitsnede zouden nemen wordt de simulatie al snel onmogelijk voor klassieke computers, terwijl diezelfde simulatie op een echte quantumcomputer in theorie mogelijk blijft.
In Hoofdstuk 3 bestuderen we de ruis die quantumberekeningen stoort. Elke fundamentele eenheid van een quantumcomputer, genaamd qubit, interacteert onvermijdelijk met zijn omgeving. Daarom ondervindt elke eenheid apart ruis. Als je een eenheid aan een quantumcomputer toevoegt, ondervindt de quantumcomputer dus als geheel meer ruis. (De totale ruis-intensiteit die een quantumcomputer ondervindt is gewoonlijk gelijk aan de ruis-intensiteit die een enkele eenheid ondervindt vermenigvuldigd met het aantal eenheden.)
Er werd echter ontdekt dat deze situatie te rooskleurig zou kunnen zijn. Er is een speciaal type ruis, genaamd super-ruis (Engels: 'super noise' of eigenlijk 'superdecoherence'), met de eigenschap dat elke eenheid die je toevoegt de ruis-intensiteit op alle reeds bestaande eenheden doet toenemen. Oftewel, hoe meer eenheden, hoe hoger de ruis-intensiteit van elk van deze eenheden afzonderlijk. (Dit betekent dat de totale ruis-intensiteit die de quantumcomputer ondervindt nu schaalt met het kwadraat van het aantal eenheden.)
Super-ruis zou een grote bedreiging kunnen vormen voor schaalbaarheid van quantumcomputers. Daarom is het essentieel dit type ruis goed te begrijpen en te bepalen wanneer het wel, en wanneer het niet optreedt. Dit doen we in Hoofdstuk 3 van dit proefschrift. Ten eerste geven we een natuurkundige interpretatie van de oorzaak van super-ruis. We laten zien dat een rij eenheden van een quantumcomputer zich effectief kan gaan gedragen als een antenne. Antennes zijn gevoelig voor elektromagnetische straling, veroorzaakt door bijvoorbeeld wifi- of radiozenders. Hoe meer eenheden een quantumcomputer heeft, hoe gevoeliger deze antenne wordt. In Hoofdstuk 3 laten we zien dat de gevoeligheid dusdanig toeneemt dat er in speciale situaties super-ruis kan ontstaan.
De antenne-analogie laat echter ook zien hoe deze super-ruis in de praktijk gewoonlijk niet voorkomt. We laten namelijk ook zien dat, hoe groter de antenne wordt, hoe meer zijn gevoeligheid zich beperkt tot een enkele frequentie. Het netto-effect van de toenemende gevoeligheid, met tegelijk een afnemende bandbreedte van die gevoeligheid, is dat er gewoonlijk geen super-ruis meer optreedt. We concluderen daarom dat super-ruis geen bedreiging vormt voor de schaalbaarheid van quantumcomputers.
In Hoofdstuk 4 bestuderen we een vorm van ruisreductie. Zoals u wellicht zelf ervaren hebt, zijn er voor een gegeven rekenprobleem meerdere manieren om bij hetzelfde, correcte antwoord uit te komen. Ook een quantumcomputer kan op verschillende manieren tot het juiste antwoord op een gegeven rekenprobleem komen. Sommige van deze manieren zijn sneller dan andere. Voor sommige van deze manieren kunnen de effecten van ruis ook minder erg zijn dan voor andere. De snelste manier is misschien niet de manier die het minste last ondervindt van ruis. Onder bepaalde omstandigheden kunnen er zelfs rekenmanieren zijn waarop ruis geen enkel effect heeft, terwijl elk van de eenheden van de quantumcomputer waarop die berekening wordt uitgevoerd wel ruis ondervindt. Zo'n rekenmanier noemen we ruisloos.
In het theoretische bewijs van het bestaan van ruisloze rekenmanieren op quantumcomputers wordt er aangenomen dat het mogelijk is perfecte kennis te hebben over de interactie tussen een quantumcomputer en zijn omgeving. In de praktijk zal deze kennis echter altijd imperfect zijn. In Hoofdstuk 4 leiden we een formule af waarmee men gemakkelijk de effecten van deze imperfectie kan kwantificeren. Met deze formule kan men dus inschatten hoe goed een ruisloze rekenmanier zich in de praktijk zal gedragen zonder deze rekenmanier daadwerkelijk uit te voeren. Dit kan bijdragen aan het verbeteren van quantumcomputers en methoden die gebruikmaken van ruisloze rekenmanieren.
Conclusie
De veeldeeltjesfysica is de studie naar het collectieve gedrag van systemen die bestaan uit vele deeltjes. Het kagome-rooster vormt een voorbeeld van zo'n veeldeeltjessysteem. Een centraal thema in dit proefschrift is de interactie tussen veeldeeltjesfysica en quantumcomputers. Deze interactie kent twee richtingen:
Door het simuleren van quantummechanische systemen kunnen quantumcomputers ons nieuwe inzichten bieden in de veeldeeltjesfysica, zoals in Hoofdstuk 2.
Hoe meer eenheden een quantumcomputer heeft, hoe meer deze quantumcomputer zelf een veeldeeltjessysteem wordt. Daarom kunnen we technieken uit de veeldeeltjesfysica gebruiken om quantumcomputers met vele eenheden te beschrijven, zoals in Hoofdstukken 3 en 4.
Er is nog een lange weg te gaan voordat quantumcomputers tot wasdom zijn gekomen. Zodra ze echter zover zijn, zal dit mogelijk een revolutie teweeg brengen in de veeldeeltjesfysica die zich kan meten met de revolutie die klassieke computers teweeg hebben gebracht in de veeldeeltjesfysica.
-
Deze pagina is gebaseerd op de introductie van mijn proefschrift. Wetenschappelijke verwijzingen heb ik hier weggelaten. Deze zijn te vinden in mijn proefschrift. ↩