Quantum computers
On the 30th of June 2021, the asteroid '2020 AD1' approached the earth with a relative velocity of approximately 17,000 km/h. Fortunately, it did not hit the earth; on the 4th of July (the date of my PhD defence), it flew by at approximately three lunar distances.12 Thanks to accurate classical simulations of the trajectory of the asteroid nobody needed to be concerned.
The solar system consist of the sun and the objects orbiting around it. Known objects include the planets, about a million of asteroids and dozens of spacecraft. Computers can simulate the solar system by creating a simplified 'board game' version of it that captures the most important aspects. In case we want to predict if an asteroid is going to hit the earth, these aspects are the velocity (including the direction) and position of the known objects in the solar system. We will henceforth call these positions and velocities, at any given time, the state of the solar system at that time. The players of the board game can be thought of as the known objects in the solar system, and the game is designed in such a way that every state of the board game corresponds to a state of the solar system. By playing many rounds of the game, a computer can find future states of the board game, and hence future states of the solar system. In this way, computers can calculate future positions of both the earth and the asteroid '2020 AD1', leading to the prediction that these two celestial bodies will not collide on the 4th of July.

Figure: The realms of classical and quantum mechanics. The way in which the world of classical mechanics emerges from the world of quantum mechanics is one of the biggest open questions in physics. As far as we can tell there is no sharp delineation between them.
The players on the board game are bound by the rules of the game. These rules are completely deterministic; there is only one valid move per player per round. This is because the rules of the game have been determined by the laws of classical mechanics, which leave no room for an element of choice. The laws of classical mechanics are the natural laws that shape our everyday experiences; if you push a pawn, it starts moving; if you let loose of a apple, it falls (Newton's law of gravitation). These same laws apply to the objects in the solar system.
To enter the world of this thesis, let us leave the solar system behind and zoom in on a tiny patch of the earth, far past the scale of planets, trees, humans, apples, pawns and microorganisms. We now enter the realm of molecules, constituting of electrons, protons and neutrons. Remarkably, different laws of nature reign here; the laws of quantum mechanics. Humans are not familiar with these laws because the objects we regularly interact with follow instead the laws of classical mechanics. Quantum mechanics can therefore be counter-intuitive and has a name for being difficult to understand.
We would also like to simulate protons, neutrons and electrons. This is because their behaviour determines chemical reactions. Hence, the simulation of protons, neutrons and electrons can help to improve industrial chemical production processes. One example is that of fertilizer. Currently, the production of one of the ingredients of fertilizer consumes about 1% of the world's total energy supply, all in the form of fossil fuels. Yet, bacteria exist that produce that same ingredient without the use of fossil fuels. If we simulated this chemical process, we could learn from the bacteria and potentially produce fertilizer more environmentally friendly.
To simulate the behaviour of electrons, protons and neutrons, we need to create a new board game, which we can call the "quantum game", that captures the essential parts of a quantum mechanical system, and let the computer play this game. The pieces of the game now represent protons, neutrons and electrons, which brings with it a change of the rules. The rules are now set by the laws of quantum mechanics. Quantum mechanics is not only difficult to humans, but also to computers; a short calculation3 shows that just to store the board game version of 37 electrons already requires at least 1 Terabyte of memory. Moreover, this requirement doubles with every electron that is added. This makes it intractable to store the simplified board game version of even a modest number of quantum mechanical particles. For example, it would require much more than all of the worlds' current data storage capacity just to store the board game version of 100 electrons. So, it seems intractable to simulate 100 electrons.
But what if we create a computer out of quantum mechanical particles themselves? Such a computer is called a quantum computer. Because the parts of a quantum computer are themselves quantum mechanical, a quantum computer can store the board game version of a quantum mechanical system more naturally than a classical computer. Furthermore, because the parts of a quantum computer follow the rules of quantum mechanics, quantum computers can apply the rules of the quantum game more naturally then a classical computer. Hence, quantum computers have been shown to be able to efficiently simulate quantum mechanical systems.


Figure: (Top) A real quantum computer. We are gazing through the window of a container all air was pumped out of (a vacuum chamber). The white contraption in the centre is used to levitate an array of 14 calcium ions (40Ca+) in its middle. Each calcium ion is a naturally occurring quantum mechanical system consisting out of 20 protons, 20 neutrons, and 19 electrons. Computations are performed by illuminating the ions with lasers whose rays pass through the windows. The program of the quantum computer determines where and when the lasers shine exactly. The output of the program is obtained by measuring which ions fluoresce and which do not. Image: C. Lackner, University of Innsbruck. (Bottom.) An array of calcium ions. In reality the width of the array is less than half a millimetre; the whole would fit on the period at the end of this sentence. Nevertheless, the ions are far apart compared to their size (~2Å); if the atoms were the size of a person, they would all be roughly 100 Km apart. Image: University of Innsbruck.
Quantum computers can do much more than playing the quantum game. The extra 'quantum power' of quantum computers can also be used to solve mathematical problems, such as the factorization of whole numbers, as it was shown by Shor. The factorization of a whole number is the task of writing that number as a product of prime numbers. Prime numbers are numbers larger than 1 that can only be divided by 1 and themselves. For example, the factorization of 15 is 3*5. Every whole number can be factored into a unique set of prime numbers. As also noted by Shor, it is widely believed that it is impossible for classical computers to efficiently factor whole numbers; small numbers (such as 15) are still doable, but classical computers quickly reach their limits. Shor was able to prove theoretically that quantum computers, on the other hand, can factorize whole numbers efficiently, and could in theory factor numbers with thousands of digits.
The potential of quantum computers to factor large numbers forms a potential threat to online security; if you can factor large numbers (e.g. with a quantum computer), you can decrypt most of the communication over the internet. The ability of a single nation state to factor large numbers before any other could have major (geo)political consequences. The search for security methods that are even unbreakable to quantum computers is an active field of research.
Despite their potential in quantum simulation and factorization, quantum computers are still in their infancy. The current state of the art is that a quantum advantage has been demonstrated on real quantum computers. This means that there have been quantum computers that performed computational tasks that are believed to be intractable on any classical computer. However, all of these computations were just 'for sports'; the task given to those quantum computers was specifically designed with the goal of showing a quantum advantage, and have no known other applications. There has not been a quantum computer that has shown a useful quantum advantage; the ability to perform a useful computation that is believed to be intractable on classical computers.
The reason that quantum computers have not yet achieved a useful quantum advantage is that it is really hard to build good quantum computers. This is because, as it turns out, it is much harder to protect quantum computers from unwanted influences from the environment than it is to protect classical computers. These influences could, for example, be magnetic fields or temperature fluctuations. In the quantum game, you can imagine the effect of these influences as a crook that comes in from outside (the environment), making a random illegal move now and then without you noticing. Then, after many rounds, the state of the board game does not faithfully represent the state of the quantum mechanical system being simulated. We call these unwanted influences noise even though they may have nothing to do with sound. To reach a useful quantum advantage in the near future, it is indispensable that we gain a thorough understanding of this noise, that we learn how to mitigate it, and that we learn how to deal with any remaining noise.
My Thesis
In Chapter 2 of my PhD thesis, we propose a task that is designed to be useful, hard for classical computers, but at the same time well-suited for quantum computers that become available in the near term. The execution of this task could have the potential of showing a useful quantum advantage on a near term quantum computer, which is an important next milestone in the development of quantum computers. The task we propose is the quantum simulation of the kagome lattice. It is a special type of simulation, where we are not so much interested in predicting future states of the kagome lattice, but rather in the task of predicting the state at temperatures close to absolute zero.
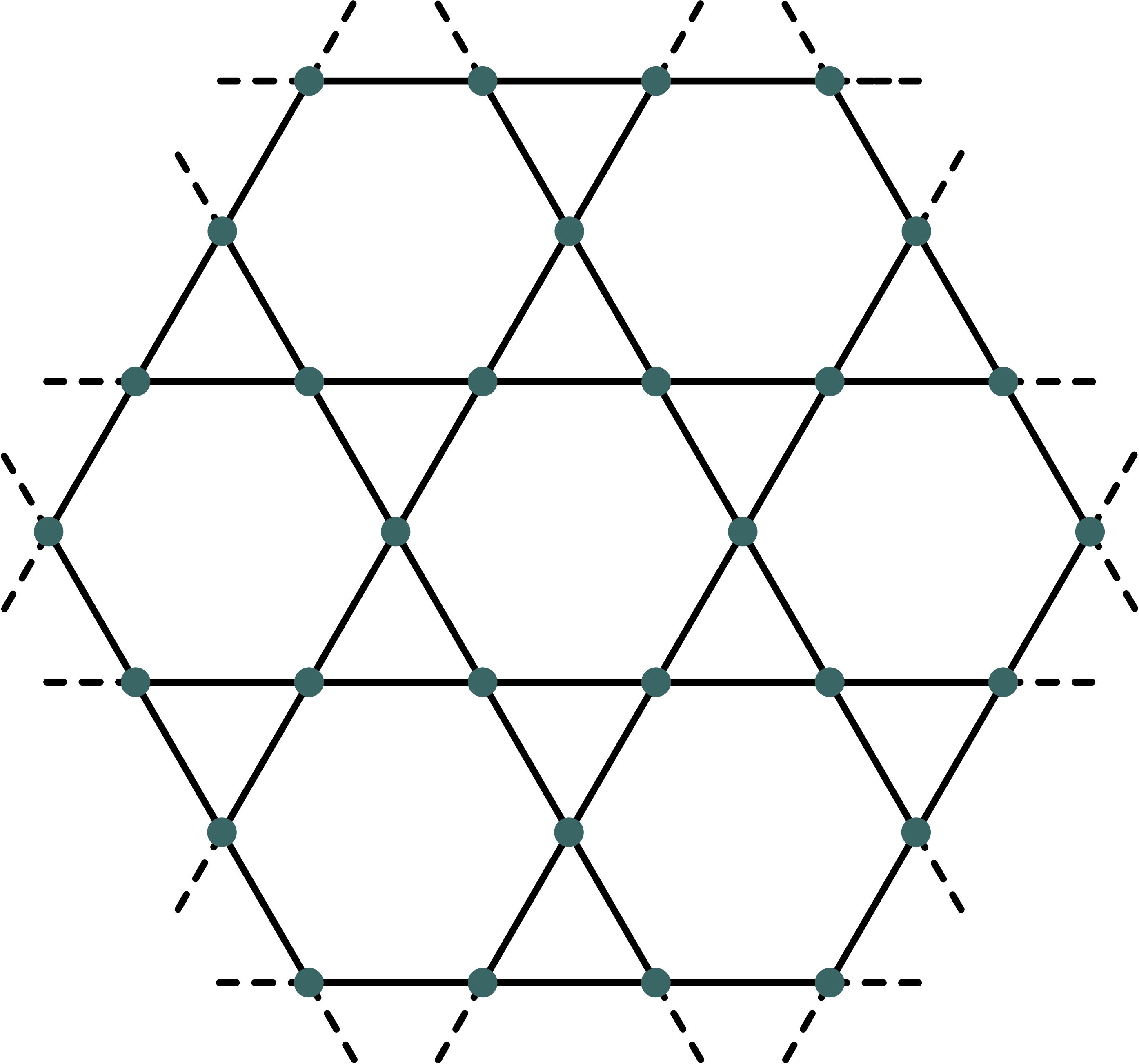

(Top) The kagome lattice. One electron is situated at every intersection. A line between two intersections depicts a magnetic interaction between the electrons it connects. It is not yet known what the state of this system is at temperatures close to absolute zero. (Bottom) Herbertsmithite, whose magnetic properties are described by electrons on the kagome lattice. Image: Bruce Kelley.
Quantum simulation of the kagome lattice can teach us new things about nature. There are materials, such as the mineral Herbertsmithite (discovered in 1972 by - you guessed it - Herbert Smith), of which the magnetic properties are described by electrons on the kagome lattice. At temperatures close to absolute zero, these properties are not yet understood. This is because the task of simulating the kagome lattice has shown to be difficult for classical computers: despite decades of research effort, the question of the properties of the state of the kagome lattice at temperatures close to absolute zero remains open to this day.
We propose a method for the quantum simulation of the kagome lattice that is adapted to the limitations of near term quantum computers. Here, we call that method the kagome quantum game. In this game, one step of one player takes the quantum computer roughly a single step of computation. This is important in near term quantum computers because their computations should take as little time as possible; the longer a computation, the more time noise has had to spoil that computation. Furthermore, the general technique of simulation we use is relatively resilient against noise.
To get an idea of how well our method would work on an ideal quantum computer, we run it on a small quantum computer. There is one catch, however: the quantum computer we run it on is not real. It is itself simulated by a classical computer. So there is a double simulation: we programmed a classical computer to simulate a quantum computer that simulates the kagome lattice. This extra step of simulation is necessary because the quantum computer we would need for testing our method does not exist yet. But, as you may ask, if researchers have not succeeded to simulate the kagome lattice on classical computers, how is it possible to simulate a quantum computer that simulates the kagome lattice, on a classical computer? The caveat is that the quantum computer simulates a tiny patch of the kagome lattice, only containing 20 electrons. The simulation of that quantum computer is still doable for classical computers. The 20-electron simulation itself would not be large enough to show a useful quantum advantage. However, if we add a couple of more electrons to the lattice, it soon becomes impossible to do the classical simulation. A quantum computer, however, could still do the simulation.
In Chapter 3, we take a closer look at the noise that hinders quantum computers. Every unit in a quantum computer (called a qubit) inevitably interacts with the environment, and hence experiences noise from that environment. We call the amount of noise a unit experiences per second the noise rate of that unit. If you add another unit to your quantum computer, the quantum computer as a whole experiences more noise. The total noise rate will be the noise rate of one unit multiplied with the number of units. It was discovered before, that in some situations, matters might even be worse. There is a special type of noise, called 'super noise' (or rather superdecoherence), with the property that every new unit you add increases the noise rate on every other single unit already in the quantum register. (This means the total noise rate of the total quantum computer now scales as the noise rate per unit times the square of the number of units.) This type of noise could pose a large threat to the feasibility of large scale quantum computers. Therefore, it is important to understand this type of noise thoroughly, and determine exactly when it occurs, and when it does not.
That is exactly what we do in Chapter 3 of my thesis. We give a physical interpretation of the origins of this 'super noise'. Namely, we show that in this setting, an array of units can effectively behave as an antenna. This is undesirable because an antenna is susceptible to electromagnetic radiation, such as radio or Wi-Fi signals. The more units your quantum computer has, the larger this antenna becomes, and hence the more sensitive it becomes. It is this increased sensitivity that leads to 'super noise'. We also show that this type of noise can be easily avoided: the larger the effective antenna becomes, the more its sensitivity concentrates on a single frequency. Thus, a quantum computer with many units only experiences super noise if there is noise on exactly the frequency the antenna tunes in to, which is something that can be avoided in practical situations. Hence, 'super noise' does not pose a real threat to quantum computers.
In Chapter 4 we study more closely a well-known method for reducing the amount of noise (including regular and super noise). As you might have experienced yourself, in solving a mathematical problem, there are multiple ways of arriving at the same, correct answer. Similarly, a quantum computer may arrive at the same answer to a problem in different ways. Some of these ways might be quicker than others. It was shown that, in theory, there exists 'noiseless ways'; these are ways where the outcome of the computation is as if no noise acted on the quantum computer (that is, the outcome is the correct outcome), even though noise did affect the individual units. A noiseless way might involve a 'detour', and hence may not be the fastest way.
In the theoretical proof of the existence of these noiseless ways, perfect knowledge of how the quantum computer reacts to the noise is assumed. In practical situations, however, perfect knowledge of how the quantum computer reacts to noise is arguably impossible. In Chapter 4, we derive a formula with which one can determine how large the effects of the imperfectness of one's knowledge are. Using this formula, one can easily determine how well a noiseless way will work in practice, aiding the design of quantum computers and quantum computational methods.
Conclusion
Many-body physics is the study of physical systems that are comprised out of many smaller units, or 'bodies'. The solar system is an example of a classical many-body system, and the kagome lattice is an example of a quantum many-body system. The central theme in this thesis is the interplay between many-body physics and quantum computation (hence its title). This interplay knows two directions:
We can use quantum computation to better understand many-body quantum physics, such as in Chapter 2.
As quantum computers are scaled up, they themselves become many-body quantum systems. Hence, we can use quantum many-body physics to better understand quantum computation, such as in Chapter 3 and Chapter 4.
There is sill a long way to go before quantum computers mature, but once they do, it has the potential to cause a revolution in physics that can match the revolution that was caused by classical computers.
-
This page is adapted from my PhD thesis. References for this page are included in the thesis, but omitted here. ↩
-
(For experts) Classical computers are not known to be able to efficiently simulate the \(N\)-body problem; the only known upper bound on the complexity of this problem is that it is in PSPACE. ↩
-
A classical description of the state of \(n\) spin degrees of freedom requires the storage of roughly \(2^n\) complex numbers. Using two floats per complex number, this takes up \(2^n\times 2 \times 4\) byte. Solving \(2^n\times 2 \times 4 \mathrm{\ byte} = 1 \mathrm{\ Terabyte}\) for \(n\) gives \(n\approx 37\). It is possible to simulate \(n\) spin degrees of freedom without storing the complete state. This requires \(\mathrm{poly}(n)\) bytes (i.e. BQP\(\subseteq\)PSPACE) However, the time complexity of this method is believed to still be exponential. ↩